디지털 신호처리(DPS)의 이해_2_STFT, Spectrogram, Mel-Spectrogram
Frequency 분석
1장에서 언급한 것처럼 우리가 일반적으로 취득할 수 있는 음성 데이터에는 다양한 주파수의 정현파(Sinusolida Signal)가 복합적으로 존재하여 복합파(Complex wave)의 형태를 유지하고 있다. 하지만 만약 여러 가지 주파수가 섞여있는 Complex wave에서 우리가 원하는 주파수의 데이터만 뽑아서 확인하고자 한다면 어떻게 찾아야 할까?
일반적으로 Complex wave에서 단일 주파수를 찾아낸다는 것은 이미 다 섞여버린 물감에서 섞기 전 물감을 찾는 것과 같은 과정이다. 따라서 우리는 생각을 전환하여 시간에 따른 amplitude값이 아닌 Frequency를 축으로 하는 그래프를 보고 불필요한 주파수의 값을 지우는 과정이 필요하다. 이를 위한 방법 중 대표적인 것이 푸리에 변환(Fourier transform)이다.
푸리에 변환(Fourier transform)
푸리에 변환(Fourier transform)을 직관적으로 설명하면 임의의 입력 신호를 다양한 주파수를 가지는 주기 함수(복수 지수 함수)의 합으로 분해하여 표현하는 것을 말한다. 그리고 각 주기 함수들의 진폭을 구하는 과정을 푸리에 변환이라고 한다.
- 주기(period) : 파동이 한번 진동하는데 걸리는 시간, 또는 그 길이. 일반적으로 sin함수의 주기는 2π/ω이다.
- 주파수(frequency) : 1초 동안의 진동 횟수
푸리에 변환 식을 살펴보자.

k는 - −∞ ∞의 범위를 가지고 움직인다. 이것은 주기 함수들의 개수이다. 어떠한 신호가 다른 주기 함수들의 합으로 표현되는데, 그 주기 함수는 무한대의 범위에 있다.
𝐴𝑘는 그 사인 함수의 진폭이다. 따라서 이 식은 시간에 대한 입력 신호 yt가 exp(𝑖⋅2𝜋𝑘/𝑇𝑡)와 진폭(𝐴𝑘)의 선형 결합으로 표현된다.
조금 더 명확히 표현하자면, 우리가 일반적으로 다루게 되는 데이터인 음악이나 목소리는 여러 개의 주파수 영역이 합쳐진 complex tone이다. 푸리에 변환은 이러한 여러 개의 주파수 영역을 분리하기 위해 사용됩니다.
하지만 여기서 드는 의문이 있다. 정현파(Sinusolida Signal)의 공식을 설명할 때는 복수 지수 함수였는데, 푸리에 변환에서는 주기 함수로 표현하는 이유는 무엇일까?
지수함수와 주기 함수의 관계를 알기 위해선 오일러 공식을 알 필요가 있다. 오일러 공식을 따르면, exponential 한 값을 sin과 cos 같은 주기 함수로 표현할 수 있음을 알 수 있다. 따라서, 푸리에 변환은 입력 signal이 어떤 것인지 상관없이 sin, cos과 같은 주기 함수들의 합으로 항상 분해 가능하다.

이 식을 푸리에 변환에 적용한다면 다음과 같다.
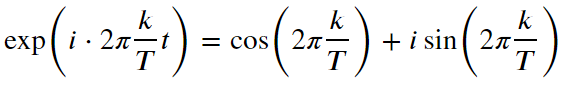
여기서 cos와 sin 함수는 주기와 주파수를 가지는 주기 함수이다. 즉, 푸리에 변환은 입력 signal이 어떤 것인지 상관없이 sin, cos과 같은 주기 함수들의 합으로 항상 분해 가능하다는 것이다.
푸리에 변환(Fourier transform)의 결과
Spectrum magnitude, phase spectrum
푸리에 변환이 끝나면, 실수부와 허수부를 가지는 복소수를 얻게 된다. 이러한 복소수의 절댓값은 Spectrum magnitude라고 부르며 주파수의 강도를 의미한다. 또한 복소수가 가지는 phase를 phase spectrum (주파수의 위상)이라고 부른다.


DFT (Discrete Fourier Transform)
Continuous to Discrete
앞서 수집한 1D array 데이터가 소리의 input이라고 하자. 이 input을 yn이라고 하고 어떠한 주기 N 으로 반복한다고 할 때, DFT는 주파수와 진폭이 다른 N개의 사인 함수의 합으로 표현이 가능하다. 앞에서 보았던 오일러 공식에 따르면, exp로 표현된 지수함수는 주기 함수의 합으로 표현할 수 있다.

위 식을 보면 k의 range가 0 부터 N - 1 로 변화했음을 알 수 있다. 이때 Spectrum Yk를 원래의 시계열 데이터에 대한 푸리에 변환 값이라고 한다.

- y_{n} : input signal
- n : Discrete time index
- k : Discrete frequency index
- Y_{k} : k번째 frequency에 대한 Spectrum의 값
def DFT(x):
N = len(x)
X = np.array([])
nv = np.arange(N)
for k in range(N):
s = np.exp(1j*2*np.pi*k/N*nv)
X = np.append(X, sum(x*np.conjugate(s)))
return X
dftcom = DFT(compsin)
STFT(Short Time Fourier Transform)
FFT는 시간의 흐름에 따라 신호의 주파수가 변했을 때, 어느 시간대의 주파수가 변하는지 모르게 된다. 이러한 한계를 극복하기 위해서 STFT는 시간의 길이를 나눠서 푸리에 변환을 하게 된다. 즉 FFT를 했을 때는 Time domain에 대한 정보가 날아가게 되는 것이다. 주파수의 특성이 시간에 따라 달라지는 사운드를 분석하는 방법이다. 일반적으로 우리가 사용하는 signal data에 적합하다. 시계열 데이터를 일정한 시간 구간 (window size)로 나누고, 각 구간에 대해서 스펙트럼을 구하는 데이터이다. 이는 Time-frequency 2차원 데이터로 표현된다.

- N : FFT size
- Window를 얼마나 많은 주파수 밴드로 나누는가 이다.
- Duration
- 샘플링 레이트를 window로 나눈 값이다.
- T=window/SR
- T(Window) = 5T(Signal), duration은 신호주기보다 5배 이상 길게 잡아야한다.
- 440Hz 신호의 window size는 5*(1/440)이 됩니다.
- w(n) : Window function
- 일반적으로 Hann window가 쓰입니다.
- n : Window size
- Window 함수에 들어가는 Sample의 양입니다.
- 작을수록 Low-frequency resolution을 가지게 되고, high-time resolution을 가집니다.
- 길수록 High-frequency, low time resolution을 가집니다.
- H : Hop size
- 윈도가 겹치는 사이즈입니다. 일반적으로는 1/4 정도를 겹치게 합니다.
STFT의 결과는 시간의 흐름(window)에 따른 frequency 영역별 amplitude를 반환한다.
# STFT
S = librosa.core.stft(audio_np, n_fft=1024, hop_length=512, win_length=1024)
S.shape, len(S[0]), S[0][0]
#input shape 중요!- n_fft : frequency 영역을 얼마만큼 줄 것인가. (N ) 보통 1024로 지정
- hop_length : 얼마큼 겹쳐서 볼 것인가.
- win_length : 하단 window function 참고 보통 n_fft와 같게 설정.
Window Function?
Window fuction은 시작 부분과 끝 부분을 0으로 만들어서 앞뒤가 이어지는 연속적인 함수로 만드는 방법이다. 하단 그래프를 예로 들자면, 가운데 그래프의 경우 처음 부분과 끝나는 부분이 다르다. 이로 인해 다음번 프레임에도 달라질 수 있기 때문에 양 끝을 같게 만들어 줄 필요가 있다. 그래서 window fuction(1번 그래프)를 2번 그래프에 곱해주게 되면 양 끝이 smothing 되는 효과를 볼 수 있다.

내용 참고: www.youtube.com/watch?v=FjYNM3YGFB4&list=PL9mhQYIlKEhem5_wrQqDtNqNcaDyFrYGN&index=2