1. Digital Signal Processing
컴퓨터가 소리를 인식하기 위해서는 컴퓨터가 이해할 수 있도록 소리를 digial signal로 표현해야 합니다 소리는 일반적으로 진동으로 인한 공기의 압축으로 생성되는데, 이 압축의 정도를 표현한 것이 Wave(파동)입니다. 파동은 진동하여 공간과 매질을 통해 전파해 나가는 현상입니다. 그리고 질량의 이동은 없지만 에너지/운동량의 운반은 존재합니다. 아래 그림을 보면 진동으로 인해 공기가 압축된 모습과, 이를 파동으로 표현한 모습을 확인할 수 있습니다.

파동이라는 것은 결국 퍼져나가기 때문에 물리량으로 볼 수 있습니다. 소리에서 얻을 수 있는 물리량은 크게 3가지가 있습니다.
- Amplitude(Intensity) : 진폭
- Frequency : 주파수
- Phase(Degress of displacement) : 위상
보통 딥러닝에서 Input data로 많이 사용되는 것은 Intensity와 Frequency입니다.
파동은 전달되는 양상을 보여주는 파라미터와, 우리의 귀에 들어왔을 때에 표현할 수 있는 파라미터가 각각 따로 존재합니다. 우리는 통상적으로 이를 물리 음향, 심리 음향이라고 합니다.
물리 음향
- Intensity : 소리 진폭의 세기
- Frequency : 소리 떨림의 빠르기
- Tone - Color : 소리 파동의 모양
심리 음향
- Loudness : 소리 크기
- Pitch : 음정, 소리의 높낮이 / 진동수
- Timbre : 음색, 소리 감각
컴퓨터가 소리를 인식하는 방법
컴퓨터가 소리를 인식하기 위해서는 아날로그 정보를 잘게 쪼개서 discrete한 디지털 정보로 표현해야 한다. 하지만 우리는 sound signal을 무한하게 쪼개서 저장할 수는 없으니 어떠한 기준을 가지고 아날로그 정보를 쪼개서 대표값을 취해야 한다. 이를 위해 우리는 연속적인 아날로그 신호를 표본화(Sampling), 양자화(Quantizing), 부호화(Encording)하여 최종적으로 이진 디지털 신호(Binary Digital Signal)로 변화시켜서 컴퓨터에 인식시키게 된다.

표본화(Sampling)단계에서 우리는 초당 샘플링 횟수를 정하는데, 이를 Sampling rate라고 한다. 다시말해서 sampling rate는 1초동안의 연속적인 시그널의 횟수를 숫자로 표현한 것이다. 잘게 쪼갤수록 원본 데이터와 거의 가까워지지만 data의 양이 증가하게 된다. 만약 너무 크게 쪼개게 된다면 원본 데이터로 복원하기 힘들어 질 수 있다.

Sampling theorm : 샘플링 레이트가 최대 frequency의 2배 보다 커져야 한다. 𝑓𝑠>2𝑓𝑚fs>2fm 여기서 𝑓𝑠fs는 sampling rate, 그리고 𝑓𝑚fm은 maximum frequency를 말한다.
- Nyqusit frequency = 𝑓𝑠/2fs/2, sampling rate의 절반.


일반적으로 sampling은 인간의 청각 영역에 맞게 형성된다.
- Audio CD : 44.1 kHz(44100 sample/second)
- Speech communication : 8 kHz(8000 sample/second)
아래는 공용 sound dataset을 사용하여 파이썬으로 샘플링 레이트를 확인해보는 코드이다.
import librosa
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
import torchaudio
# tra
#in_dataset = torchaudio.datasets.LIBRISPEECH("./", url="train-clean-100", download=True)
test_dataset = torchaudio.datasets.LIBRISPEECH("./", url="test-clean", download=True)
test_dataset[1] #소리 데이터, 샘플레이트
test_dataset[0][0].shape
audioData = test_dataset[1][0][0]
sr = test_dataset[1][1]
print(audioData, audioData.shape)
len(audioData)
len(audioData) / sr #duration이 나옴
import IPython.display as ipd
ipd.Audio(audioData, rate=sr)
양자화(Quantizing)단계에서는 amplitude의 real valued를 기준으로 시그널의 값을 조절한다. 양자화 하기 위해서 우리는 Amplitude를 이산적인 구간으로 나누고, Signal data의 Amplitude를 반올림한다. 이 과정을 통해 우리는 네트워크 효율과 용량 효율의 증대를 기대할 수 있다. 만약 dataset의 크기가 클 경우에는 Sampling rate를 조절하는 것이 유효하다.

그렇다면 이산적인 구간은 어떻게 나눌수 있을까? 이는 bit의 비트에 의해서 결정된다.
- B bit의 Quantization : −2𝐵−1−2B−1 ~ 2𝐵−1−12B−1−1
- Audio CD의 Quantization (16 bits) : −215−215 ~ 215−1215−1
- 위 값들은 보통 -1.0 ~ 1.0 영역으로 scaling되기도 한다.
아래는 파이썬을 통해 음성파일을 Quantization 하는 코드이다.
audio_np = audioData.numpy()
normed_wav = audio_np / max(np.abs(audio_np))
ipd.Audio(normed_wav, rate=sr)
#quantization 하면 음질은 떨어지지만 light한 자료형이 된다.
Bit = 8
max_value = 2 ** (Bit-1)
quantized_8_wav = normed_wav * max_value
quantized_8_wav = np.round(quantized_8_wav).astype(int)
quantized_8_wav = np.clip(quantized_8_wav, -max_value, max_value-1)
ipd.Audio(quantized_8_wav, rate=sr)
부호화(Encording)단계에서는 value간의 분별력을 만들기 위해 wave의 value를 정형화 하는 작업을 진행한다. 사람의 귀는 소리의 Amplitude에 대해서 log적으로 반응한다. 즉, 작은 소리의 차이는 잘 잡아내는데에 반해 소리가 커질수록 그 차이를 잘 느끼지 못한다. 이러한 특성을 wave값 표현에 반영하여 작은값에는 높은 분별력(high resolution)을, 큰값끼리는 낮은 분별력(low resolution)을 갖게 한다.

def mu_law(x, mu=255):
return np.sign(x) * np.log(1 + mu * np.abs(x)) / np.log(1 + mu)
x = np.linspace(-1, 1, 1000)
x_mu = mu_law(x)
plt.figure(figsize=[6, 4])
plt.plot(x)
plt.plot(x_mu)
plt.show()
Frequency란?
얼마나 압축되었는지(The number of compressed)를 뜻한다. 단위는 Hertz를 사용하며, 1Hertz는 '1초에 한번 Vibration'을 의미합니다. 이와 관련된 용어로 주기와 주파수가 있습니다.
- 주기(period) : 파동이 한번 진동하는데 걸리는 시간, 또는 그 길이. (일반적으로 sin함수의 주기는 2π/w 이다.)
- 주파수(frequency) : 1초 동안의 진동 횟수.
주파수가 높을 수록 파동의 주기가 짧아지며, 높은 주파수에서는 높은 소리, 낮은 주파수에서는 낮은 소리가 난다.


Complex Wave?
우리가 사용하는 대부분의 소리들은 단일한 Frequenccy가 아닌복수의 서로 다른 정현파들의 합으로 이루어진 복합파(Complex Wave)이다.

Sinusoidal Wave?
모든 신호는 주파수(frequency)와 크기(magnitude), 위상(phase)이 다른 정현파(sinusolida signal)의 조합으로 나타낼 수 있다. 정현파는 일종의 복소 주기함수이며 복수 주기함수는 복소수가 있는 주기함수를 뜻한다. 복소수 영역이 Phase 영역이고 주파수 영역이 Frequency 영역이다. 이들의 크기를 담당하는 것이 Amplitude이다.
정현파는 아래의 수식처럼 나타낼 수 있다.
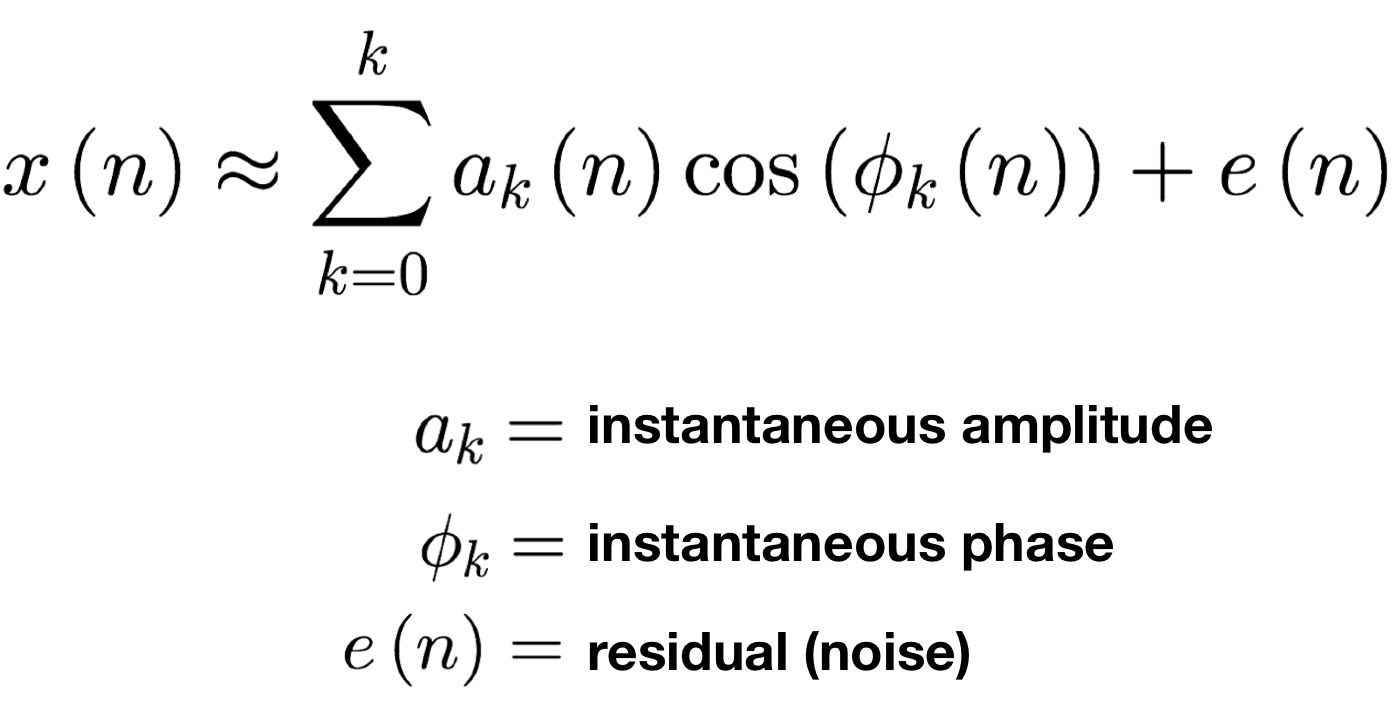
또한 위 수식을 파이썬에서 모델링하기 위해서 아래와 같이 적용한다.

- t/fs : Frequency와 Time에 관련된 영역
- amplitude 영역은 Int값으로 넣을 수 있고
- cos 함수는 numpy를 통해 함수를 불러올 수 있고,
- cos안에 phase를 넣어줄 수 있다.
위의 내용을 바탕으로 파이썬에서 '라' 음계의 정현파를 만들 수 있다.
A = 0.9 #Amplitude
f = 340 #Frequency 계이름 '라'
phi = np.pi/2 #Phase
fs = 22050 #
t = 1 # time _ 1초
#여러개의 정현파를 합치면 소리의 신호. 반대로 소리에서 정현파를 분리할 수 있다.
def Sinusoid(A,f,phi,fs,t):
t = np.arange(0,t,1.0/fs)
x = A * np.cos(2*np.pi*f*t+phi)
return x
sin2 = Sinusoid(A,f,phi,fs,t)
sin2
ipd.Audio(sin2, rate=fs)
위의 코드로 만들어진 정현파에 다른 음계의 정현파를 추가하여 복합파를 만들어 낼 수 있다. 아래 코드에서 추가로 만드는 sin 정현파는 sampling rate가 같기 때문에 시간을 동일하게 하면 동일한 길이의 파장대를 만들 수 있다.
sin = Sinusoid(1.2,720,phi,fs,t)
sin
complexwave = sin + sin2
import librosa.display
S = librosa.feature.melspectrogram(complexwave, sr=fs, n_mels = 128)
log_S = librosa.power_to_db(S, ref=np.max)
plt.figure(figsize=(12,4))
librosa.display.specshow(log_S, sr=sr, x_axis='time', y_axis='log')
plt.title('Mel power sepctrogram')
plt.colorbar(format='%+02.0f dB')
plt.tight_layout()
위의 그래프를 확인해보면 2개의 정현파를 합쳐놓았기 때문에 2개의 frequency가 나타나는 것을 확인할 수 있다.
내용 참고: www.youtube.com/watch?v=RxbkEjV7c0o&list=PL9mhQYIlKEhem5_wrQqDtNqNcaDyFrYGN&index=1
Reference
- Digital Signal Processing Lecture https://github.com/spatialaudio/digital-signal-processing-lecture
- Python for Signal Processing (unipingco) https://github.com/unpingco/Python-for-Signal-Processing
- Audio for Deep Learning (남기현님) https://tykimos.github.io/2019/07/04/ISS_2nd_Deep_Learning_Conference_All_Together/
- 오디오 전처리 작업을 위한 연습 (박수철님) https://github.com/scpark20/audio-preprocessing-practice
- Musical Applications of Machine Learning https://mac.kaist.ac.kr/~juhan/gct634/
- Awesome audio study materials for Korean (최근우님) https://github.com/keunwoochoi/awesome-audio-study-materials-for-korean
'신호처리' 카테고리의 다른 글
| 디지털 신호처리(DPS)의 이해_2_STFT, Spectrogram, Mel-Spectrogram (0) | 2021.02.18 |
|---|